Chapter 13 回帰分析の応用

13.1 変数の変換

13.1.1 測定単位の変更

前の章の例を使ってみよう。

model1 <- feols(sales ~ ads + age + income, data = dat_sim)
model2 <- feols(sales ~ ads + age + I(income*10000), data = dat_sim)

etable(model1,model2)

##                               model1               model2
## Dependent Var.:      支店の売上      支店の売上
##                                                          
## Constant            499.6*** (6.860)     499.6*** (6.860)
## 広告ダミー     49.66*** (4.028)     49.66*** (4.028)
## 店長の年齢(歳)  4.985*** (0.1299)    4.985*** (0.1299)
## 地域の平均所得(万円) 0.0899*** (0.0078)                     
## I(income x 10000)                    8.99e-6*** (7.81e-7)
## _________________ __________________ ____________________
## S.E. type                        IID                  IID
## Observations                     300                  300
## R2                           0.92132              0.92132
## Adj. R2                      0.92052              0.92052
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

上では、全く同じモデルを推定しているが、違いはincomeの単位である。データの中では、incomeの単位は「万円」で記録されている。例えば数値が200であったら、200万円という意味である。

そのデータに10000をかけているので、２つ目のモデルでは単位が「円」になっている。

見ての通り、このデータの単位の変換を行ったところで、データのばらつきは同じなので他の係数の推定にも影響はない。所得の係数の推定値は非常に小さくなっているが、これは解釈の違いに影響する。

１つ目のモデルでは、「所得が1万円上昇すると、0.0899万円売上が上昇する」という解釈になる。しかし、2つ目のモデルでは「所得が1円上昇すると、0.00000089万円売上が上昇する」となる。

どちらがわかりやすいだろうか？

13.1.2 中心化

13.1.3 対数変換

対数変換とは文字通り、変数の対数を取ることである。ことわりがない限り、自然対数を意味している場合が多い。自然対数とは対数の底がネイピア数（Napier’s constant）である。

ある変数Xに対して、\(\log_eX\)が対数変換である。自然対数は\(\ln X\)とも表記される。

13.1.3.1 対数

13.1.3.2 対数変換を用いたモデルの種類

13.1.3.3 (発展) 対数化とパーセントの近似

被説明変数（目的変数）を対数変換したモデルは \[ \log(y_i) = \alpha + \beta_1 x_i + \varepsilon_i \]

\(x\)を\(\Delta x\)だけ増やした時に、yが\(\Delta y\)だけ増えるとすると、 \[ \log(y_i + \Delta y_i) = \alpha + \beta_1 (x_i+\Delta x_i) + \varepsilon_i \]

この増えた式を元の式から引くと、 \[ \log(y_i + \Delta y_i) - \log(y_i) = \alpha + \beta_1 (x_i+\Delta x_i) + \varepsilon_i - (\alpha + \beta_1 x_i + \varepsilon_i) = \beta_1 \Delta x_i \]

このとき、左辺は \[ \begin{align} \log(y_i + \Delta y_i) - \log(y_i) & = \log(\frac{y_i + \Delta y_i}{y_i}) \\ & = \log(1 + \frac{\Delta y_i}{y_i}) \\ & \approx \frac{\Delta y_i}{y_i} \end{align} \] となる。ここで１つ目の等式は、対数の公式：\(\log(x)-\log(y) = \log(x/y)\)を用いている。また、３つ目の近似はテイラー展開を用いた近似であり、\(a\)の値が十分に小さい時に、\(\log(1+a) \approx a\)であることが知られている。気になる人は、例えばlog(1 + 0.1)をRで実行してみよう。

つまり、 \[ \frac{\Delta y_i}{y_i} \approx \beta_1 \Delta x_i \] が成り立つことからxの微小な変化によるyの相対的な変化(%変化)が\(\beta_1\)で表されることがわかる。

13.1.4 変数の単位と、傾きパラメータの解釈

回帰分析の係数の解釈は、その説明変数が１単位増えたときに、目的変数がどれだけ変化するか、である。

例えば、以下のようなモデルがあるとする。

\[ 賃金_i = \alpha + \beta_1 経験年数_i + \varepsilon_i \]

このとき推定された\(\hat{\beta_1}\)の解釈は「教育年数が１年増えると賃金が\(\hat{\beta_1}\)上がる」となる。この「説明変数が１単位増えた場合の目的変数への効果」を限界効果と呼ぶ。

この限界効果は、モデルを微分することでも得ることができる。一般的な単回帰モデルは以下のように記述される。

\[ y_i = \alpha + \beta_1 x_i + \varepsilon_i \]

このモデルを説明変数\(x_i\)で微分したもの \[ \frac{dy}{dx} = \beta_1 \]

微分は、xの微小な変化によるyの変化量として解釈される。その変化量が\(\beta_1\)となる。

13.2 より複雑な効果をモデル化

13.2.1 関数形の変更：二次関数

上のモデルでは、経験年数が１年増えた場合の賃金への効果は常に一定で\(\hat{\beta_1}\)であるという解釈になる。

しかし、もっと複雑かつ柔軟なモデル化も可能である。例えば、仕事の経験年数が浅いときに１年経験が増えた後に増加する賃金は大きいかもしれないが、経験年数が多く経った時に１年経験が増えたところで大きく賃金は増加しないかもしれない。

そのような形の限界効果をモデル化するには、回帰モデルの形を変更することで対処できる。

\[ y_i = \alpha + \beta_1 x_i + \beta_2 x^2_i +\varepsilon_i \]

このモデルを上と同じく微分すると

\[ \frac{dy}{dx} = \beta_1 + 2\beta_2x_i \]

となる。先ほどと違い、限界効果の中に\(x_i\)が入っているということは、効果の量が\(x_i\)の量によって異なるということである。

dat_funplot = tibble(
  x = seq(0,10,by=0.1),
  y1 = 3 + 0.2*x,
  y2 = 3 + 0.35*x - 0.02*x^2
)

ggplot(dat_funplot, aes(x=x)) + 
  geom_line(aes(y=y1), col="red") + 
  geom_line(aes(y=y2), col="blue") +
  annotate("text",x=7.5,y=4.75,parse=TRUE, 
           label="y==alpha+beta[1]*x", col="red") +
  annotate("text",x=5.0,y=4.5,parse=TRUE, 
           label="y==alpha+beta[1]*x+beta[2]*x^2", col="blue") +
  labs(x="x", y ="y") +
  theme_bw()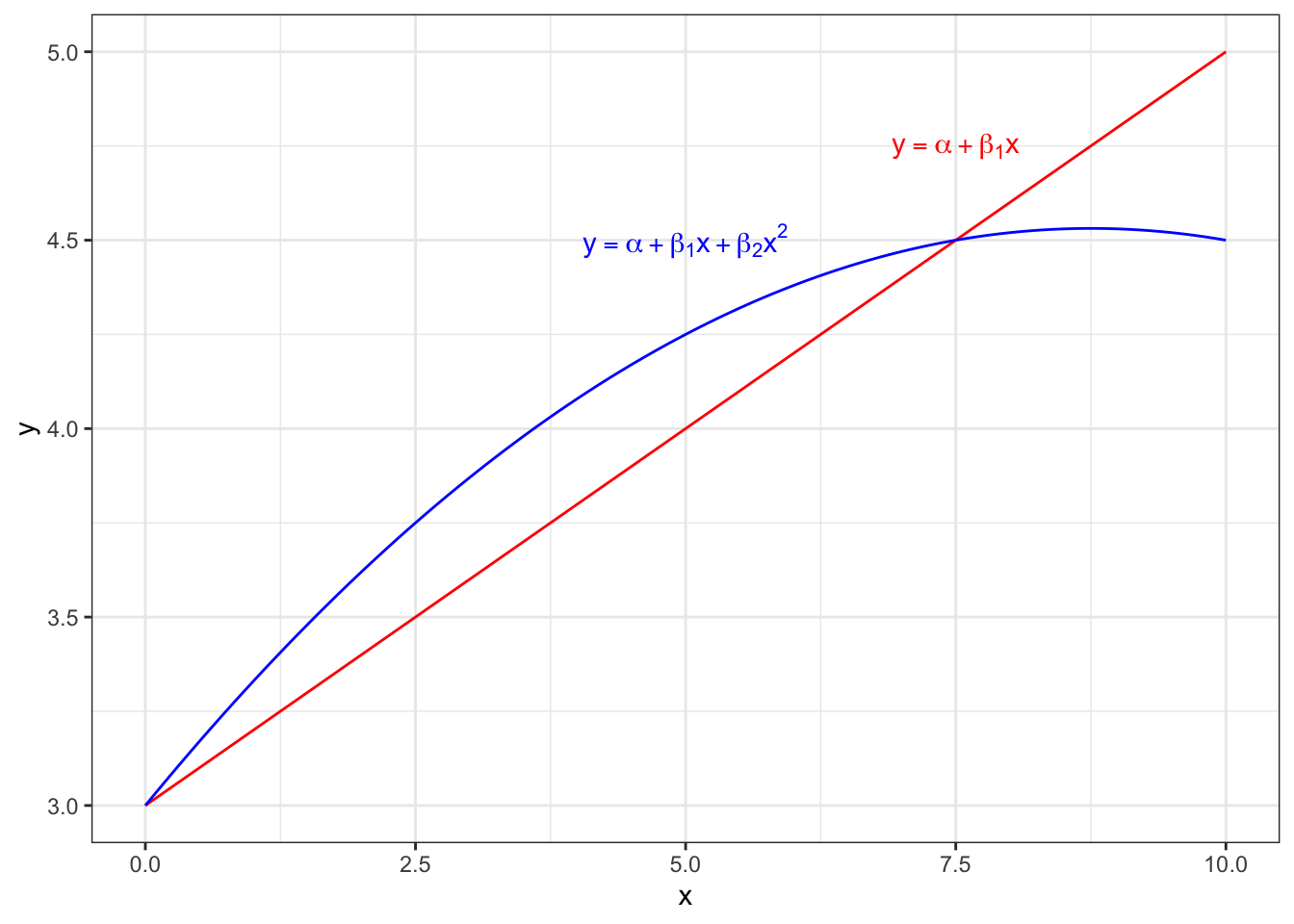

13.2.2 例：経験年数の年収への効果

以下のようなモデルを推定する。

\[ 対数賃金_i = \alpha + \beta_1 経験年数_i + \beta_2 経験年数^2_i + \beta_3 教育年数 + \varepsilon_i \] 左辺が対数の場合は限界効果の解釈はxが１単位増加した時に、目的変数が何％増加するか、になる。

13.2.2.1 準備

multi_reg_app.Rというスクリプトを準備し、必要なパッケージをロードする。

library(tidyverse)
library(fixest)
library(skimr)

13.2.2.2 データのロード

以下の通りデータをダウンロードして、読み込む。

# データのダウンロードとdataフォルダへの保存
download.file("https://github.com/keita43a/regression_tutorial/blob/main/data/dat_income.csv?raw=TRUE",
              destfile="data/dat_income.csv")

dat_income = read_csv("data/dat_income.csv")

13.2.2.3 データの確認

skim(dat_income)

Table 13.1: Data summary
Name	dat_income
Number of rows	4299
Number of columns	4
_______________________
Column type frequency:
numeric	4
________________________
Group variables	None

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
exper	1	11.82	6.28	0.00	7.00	12.00	17.00	26.00	▆▇▇▇▃
yeduc	1	13.86	1.88	9.00	12.00	13.00	16.00	18.00	▁▇▇▇▁
income	1	264.82	179.91	6.25	150.00	250.00	350.00	2250.00	▇▁▁▁▁
lincome	1	5.29	0.90	1.83	5.01	5.52	5.86	7.72	▁▂▅▇▁

13.2.2.4 推定

reg_income <- feols(lincome ~ exper + I(exper^2) + yeduc, data=dat_income)

etable(reg_income)

##                          reg_income
## Dependent Var.:             lincome
##                                    
## Constant          2.486*** (0.1108)
## exper            0.1962*** (0.0075)
## exper square    -0.0064*** (0.0003)
## yeduc            0.1175*** (0.0071)
## _______________ ___________________
## S.E. type                       IID
## Observations                  4,299
## R2                          0.20660
## Adj. R2                     0.20605
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

例えば経験年数が5年ならば、限界効果は13.6%となり、10ならば7.6%となる。

\[ \frac{d対数賃金}{d経験年数}|_{経験年数=5} = 0.196 - 2\times0.006\times5 =0.136 \]

\[ \frac{d対数賃金}{d経験年数}|_{経験年数=10} = 0.196 - 2\times0.006\times10 =0.076 \]

0.196-2*0.006*5

## [1] 0.136

0.196-2*0.006*10

## [1] 0.076

13.2.3 ダミー変数を使った分析

\[ 対数賃金_i = \alpha + \beta_1 教育年数 + \beta_2 女性ダミー_i + \varepsilon_i \]

# データのダウンロードとdataフォルダへの保存
download.file("https://github.com/keita43a/regression_tutorial/blob/main/data/dat_income_female.csv?raw=TRUE",
              destfile="data/dat_income_female.csv")

dat_income_female <- read_csv("data/dat_income_female.csv")

skim(dat_income_female)

Table 13.2: Data summary
Name	dat_income_female
Number of rows	4286
Number of columns	3
_______________________
Column type frequency:
numeric	3
________________________
Group variables	None

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
female	1	0.50	0.50	0.00	0.00	0.00	1.00	1.0	▇▁▁▁▇
yeduc	1	13.86	1.88	9.00	12.00	14.00	16.00	18.0	▁▇▇▇▁
lincome	1	5.26	0.94	1.83	4.83	5.52	5.86	7.3	▁▂▃▇▂

reg_income_female <- feols(lincome ~ yeduc + female, data=dat_income_female)

etable(reg_income_female)

##                   reg_income_female
## Dependent Var.:             lincome
##                                    
## Constant          4.863*** (0.0961)
## yeduc            0.0586*** (0.0067)
## female          -0.8321*** (0.0254)
## _______________ ___________________
## S.E. type                       IID
## Observations                  4,286
## R2                          0.22027
## Adj. R2                     0.21991
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

13.2.4 交差項

\[ 対数賃金_i = \alpha + \beta_1 教育年数_i + \beta_2 女性ダミー_i + \beta_3 女性ダミー_i\times教育年数_i + \varepsilon_i \]

reg_income_female_2 <- feols(lincome ~ yeduc + female + yeduc:female, data=dat_income_female)

etable(reg_income_female_2)

##                 reg_income_fema..2
## Dependent Var.:            lincome
##                                   
## Constant         5.347*** (0.1209)
## yeduc            0.0241** (0.0085)
## female          -2.079*** (0.1924)
## yeduc x female  0.0902*** (0.0138)
## _______________ __________________
## S.E. type                      IID
## Observations                 4,286
## R2                         0.22798
## Adj. R2                    0.22744
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1